Question

Using these coordinates, (3, 1/4) and (-2, -1) write an equation in Point-Slope, Slope-Intercept, and Standard Form.

Answer 1

Answer here
`\text{Slope } = \frac{ y_2 - y_1 } { x_2 - x_1 } = (-1 - (1)/(4))/(-2 - 3) = ( - (5)/(4))/(-5)= ( - (5)/(4)\cdot4)/(-5\cdot4) =(-5)/( -20) =\boxed{ \bf{ (1)/(4)}}`

The slope is 1/4.

The equation in point-slope form is:
y - (-1) = 1/4(x - (-2))

`\boxed{\bf{y + 1 = (1)/(4)(x+2)}}`

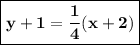
In slope-intercept form, it is:
y + 1 = 1/4(x+2)

`\boxed{\bf{y = (1)/(4)x - (1)/(2)}}`

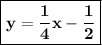
In Standard form it is:
y = 1/4x - 1/2
1/2 = 1/4x - y
Multiply both sides by 4
2 = x - 4y

`\boxed{\bf{x-4y=2}}`

I hope that helps. :)