Question

1)log2 32+lne-lg100
2) log3 x + 4 log9 x= 9

Answer 1

1.log2 32=5
lne=1
lg100=2
5+1-2=4
2. 4log9 x= 2log3 x=log3 x^2
log3 x*x^2=9
log3 x^3=9
log 3 x=3
x=27

Answer 2

To simplify we need recall and apply the properties and laws of logarithms.

1)


`log_(2)(32) + ln(e) + log_(10)(100)`


`log_(2)(32) + log_(e)(e) + log_(10)(100)`

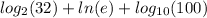
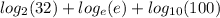
We need consider the base of each logarithm and express the numbers in the parentheses to each base raised to a certain index. or exponent.

That is

`{2}^(5) = 32 \\ \\ {10}^(2) = 100`

As for the middle expression, the base and the number are equal so let us keep it for now.

Our expression now becomes,


`log_(2)( {2}^(5) ) + log_(e)(e) + log_(10)( {10}^(2) )`

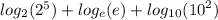
Recall this law of logarithm,


`log_(a)( {m}^(n) ) = n log_(a)(m)`


`5 log_(2)( {2}) + log_(e)(e) + 2log_(10)( {10} )`

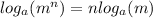
Recall again that,


`log_(a)(a) ,a \\e0 \: or \: 1`

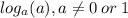
Therefore our expression becomes,

`5 (1) + (1) + 2(1) = 5 + 1 + 2 = 8`

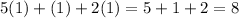
2) We use change of base to solve this logarithmic equation.


`log_(3)(x) + 4log_(9)(x) = 9`


`log_(3)(x) + log_(9)( {x}^(4) ) = 9`

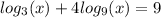
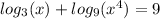
It will be easier and faster to change the base to 3.
Recall that,


`\log_(x)(y)=(log_(a)(y))/(log_(a)(x))`

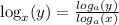
We apply this law to obtain,


`log_(3)(x) + \frac{log_(3)( {x}^(4))}{log_(3)(9) } = 9`


`log_(3)(x) + \frac{log_(3)( {x}^(4))}{log_(3)( {3}^(2) ) } = 9`


`log_(3)(x) + \frac{log_(3)( {x}^(4))}{2log_(3)( {3} ) } = 9`


`log_(3)(x) + \frac{log_(3)( {x}^(4))}{2(1) } = 9`


`log_(3)(x) + \frac{log_(3)( {x}^(4))}{2} = 9`

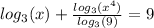
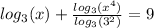
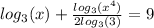
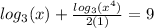
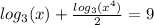
multiplying through by 2 gives,


`2log_(3)(x) + log_(3)( {x}^(4) ) = 18`


`log_(3)( {x}^(2) ) + log_(3)( {x}^(4) ) = 18`


`log_(3)( {x}^(4) * {x}^(2) ) = 18`

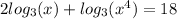
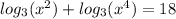
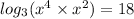
We apply the multiplication law of exponents to obtain,


`log_(3)( {x}^(4 + 2) ) = 18`


`log_(3)( {x}^(6) ) = 18`
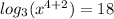
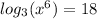
We take antilogarithms to get,


`{x}^(6) = {3}^(18)`


`{x}^(6) = ( {3}^(3) ) ^(6)`


`x = {3}^(3)`

`x = 27`

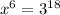
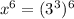
Hence x is 27.