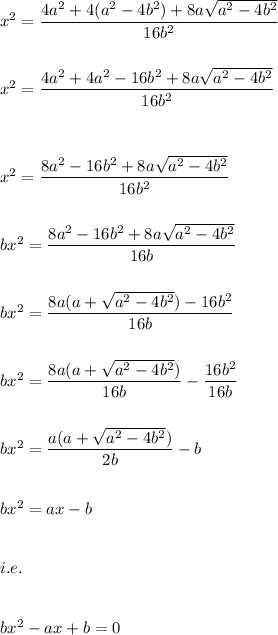Answer with explanation:
Ques 1)
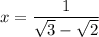
Now we are asked to find the value of:
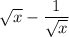
We know that:
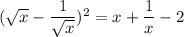
Also:
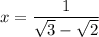 could be written as:
could be written as:
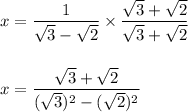
since, we know that:
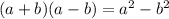
Hence,
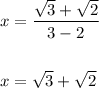
Also,
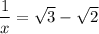
Hence, we get:
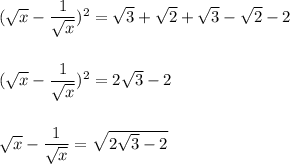
Hence,
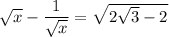
Ques 2)
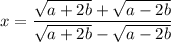
on multiplying and dividing by conjugate of denominator we get:
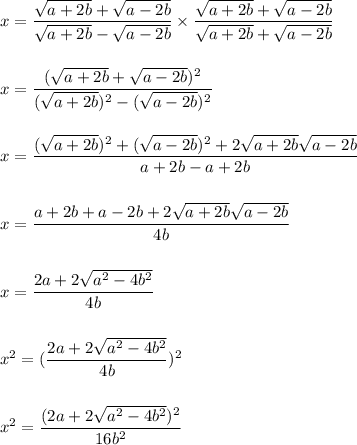
Hence, we have: