We have a mixture of 300 ml with 15% alcohol content, this means that in this mixture we have an alcohol total of:
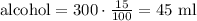
And we want to obtain a 60% alcohol solution by mixing a 90% mixture with the 15% one we have.
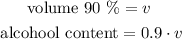
When we add this volume to what we already have, we will obtain:

And what we want is that the alcohol content must be equal to 60% of the final mixture, so we have:
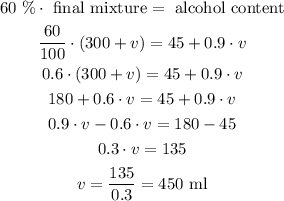
This means that we need to add 450 ml of the 90% solution to obtain the desired final mixture.