Question

Which statement best describes how the volume of a cube changes when the edge length is doubled to form a new cube?A. the volume of the new cube is 1/2 the volume of the original cube.B. the volume of the new cube is 1/4 the volume of the original cube. C. the volume of the new cube is 8 times the volume of the original cube.D. The volume of the new cube is 4 times the volume of the original cube.

Answer 1

Let's call the original length of the side of the cube "l".

When the side is l, the volume of the cube is:

`V_{\text{original}}=l^3`

Now, since the length of the side of the cube must double, let's calculate what will the volume be when the length instead of "l" is "2l". As we did for the first volume, we raise to the third power the measure of the side, and since this time the measure of the side is 2l, the new volume is:

`V_{\text{new}}=(2l)^3`

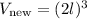
We solve this expression as follows:

`\begin{gathered} V_{\text{new}}=2^3l^3 \\ V_{\text{new}}=8l^3 \end{gathered}`

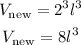
Remember that the original volume was

`V_{\text{original}}=l^3`

Thus, the new volume defined in terms of the original volume is:

`V_{\text{new}}=8\cdot V_{\text{original}}`

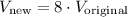
The volume of the new cube is 8 times the volume of the original cube.

Answer: C