so quadatic equation is
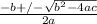
=x
since there are no fraction parts, the 2a part mus cancel
for simplicity, assume that a=1
therefor the 2a part simplifies to 1
replace all a's with 1
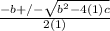
=x
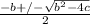
=x
-b must equal 2 times 8 since the whole thing is divided by 2
therefore b=-16
subsitue
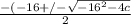
=x
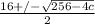
=x
since the i is 1i that means that the simplified square root is equal to 2i so therefor the inside must result in -4
256-4c=-4
add 4c to both sides
256=4c-4
add 4 to both sides
260=4c
divide both sides by 4
65=c
the equation is x^2-16b+65=0