Question

A forest ranger sights a fire directly to the south. A second ranger, 10 miles east of the first ranger, also sights the fire. The bearing from the second ranger to the fire is S 35° W. How far is the first ranger from the fire?

Answer 1

The problem can be depicted in figure as:

The first ranger sight fire to south from A to C

The second ranger sights fire at east of first ranger at a distance 10 miles

Thus,

`_(\angle SBC=35^o)`

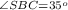
Thus,

`\angle ABC=90^o-35^o=55^o`

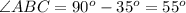
In triangle ABC,

`\text{tan}55^o=(AC)/(AB)`
`1.42=(AC)/(10)`
`AC=14.2\text{miles}`

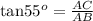
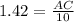
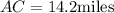
So the first ranger is at a distance 14.2 miles from the fire.