The problem can be depicted in figure as:
The first ranger sight fire to south from A to C
The second ranger sights fire at east of first ranger at a distance 10 miles
Thus,
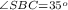
Thus,
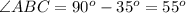
In triangle ABC,

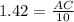
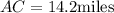
So the first ranger is at a distance 14.2 miles from the fire.