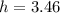We are given that the shorter leg of a 30 60 90 triangle measures a square root of 3. We are asked to find the hypothenuse. To do that, let's first draw a diagram of the problem.
As we can observe in the diagram the shorter leg refers to the side that is opposite to the 30 degrees angle since in any triangle the shortest side is always opposite to the shorter angle. To find the hypotenuse we use the function sine of 30 degrees since this function is defined as follows:
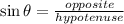
replacing the known values:
![\sin 30=\frac{\sqrt[]{3}}{h}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/y3nfguj7i81ej2819dtm.png)
where "h" is the hypotenuse. Solving for "h" we get:
![h\sin 30=\sqrt[]{3}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/9aqw7dmecpyb50hmxky9.png)
Dividing both sides by sin30
![h=\frac{\sqrt[]{3}}{\sin 30}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/aak6l6m5yz6s5fmiw2yr.png)
From trigonometry, we know the following value for the sine of 30
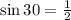
replacing in the equation:
![h=\frac{\sqrt[]{3}}{(1)/(2)}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/b06ye7qh8igql4sr1jdw.png)
Solving the operations:
![h=2\sqrt[]{3}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/un12og1mo3kh8vsr1qqc.png)
in decimal notation, this is equal to: