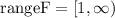To make the table of values we need to determine in which interval we need to use each of the expressions of the piecewise function. For any value less than zero we need to use the expression y=3. For any value greater or equal than zero we are going to use the expression x+1; with this in mind we have the following table:
Now that we have this table we plot the points given and graph the function:
Now, in here it is important to notice that the horizontal lines goes till x=0 BUT we draw a hollow point indicating that this line does not touch the zero, this measn that the function y=3 is defined for x<0 like the function stated.
Furthermore we have to draw a solid circle in the point (0,1) that indicates that the function takes that value when x=0.
Now from the graph we notice that the function is defines for all values of x then we have that the domain is:
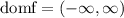
Also from the graph we notice that the range is the interval: