Question

If cos A = 1/3 with A in QIV, then sin A/2=

Answer 1

The question gives us the value of

`\cos A=(1)/(3)`

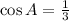
We are then required to find

`\sin ((A)/(2))`

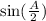
In order to find the value of this expression, we need to use the following trigonometric identity:

`\begin{gathered} \cos A=\cos ^2((A)/(2))-\sin ^2((A)/(2)) \\ \\ \cos ^2((A)/(2))=1-\sin ^2((A)/(2)) \\ \\ \therefore\cos A=1-\sin ^2((A)/(2))-\sin ^2((A)/(2)) \\ \cos A=1-2\sin ^2((A)/(2)) \end{gathered}`

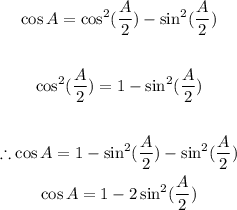
With this derived identity for cos A, we can proceed to solve the question.

The identity expresses cos A in terms of sin (A/2). Since we already know the value for cos A, we can proceed to find

the value of sin(A/2)

This is done below:

`\begin{gathered} \cos A=1-2\sin ^2((A)/(2)) \\ \\ \text{Making sin(}(A)/(2))\text{ the subject of the formula;} \\ \text{subtract 1 from both sides}S \\ \cos A-1=-2\sin ^2((A)/(2)) \\ \\ \text{Divide both sides by -2} \\ (\cos A-1)/(-2)=\sin ^2((A)/(2)) \\ \\ \text{ Find the square root of both sides} \\ \\ \therefore\sin ((A)/(2))=\sqrt[]{(\cos A-1)/(-2)} \end{gathered}`

Now that we have the final expression for calculating sin(A/2), let us substitute the value of cos A into the expression.

This is done below:

`\begin{gathered} \sin ((A)/(2))=\sqrt[]{(\cos A-1)/(-2)} \\ \cos A=(1)/(3) \\ \\ \sin ((A)/(2))=\sqrt[]{((1)/(3)-1)/(-2)} \\ \\ \sin ((A)/(2))=\sqrt[]{(1)/(3)} \\ \\ \end{gathered}`