The question gives us the value of

We are then required to find
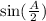
In order to find the value of this expression, we need to use the following trigonometric identity:
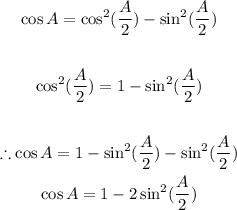
With this derived identity for cos A, we can proceed to solve the question.
The identity expresses cos A in terms of sin (A/2). Since we already know the value for cos A, we can proceed to find
the value of sin(A/2)
This is done below:
![\begin{gathered} \cos A=1-2\sin ^2((A)/(2)) \\ \\ \text{Making sin(}(A)/(2))\text{ the subject of the formula;} \\ \text{subtract 1 from both sides}S \\ \cos A-1=-2\sin ^2((A)/(2)) \\ \\ \text{Divide both sides by -2} \\ (\cos A-1)/(-2)=\sin ^2((A)/(2)) \\ \\ \text{ Find the square root of both sides} \\ \\ \therefore\sin ((A)/(2))=\sqrt[]{(\cos A-1)/(-2)} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/zrpmo7fb98enyv3gqt39.png)
Now that we have the final expression for calculating sin(A/2), let us substitute the value of cos A into the expression.
This is done below:
![\begin{gathered} \sin ((A)/(2))=\sqrt[]{(\cos A-1)/(-2)} \\ \cos A=(1)/(3) \\ \\ \sin ((A)/(2))=\sqrt[]{((1)/(3)-1)/(-2)} \\ \\ \sin ((A)/(2))=\sqrt[]{(1)/(3)} \\ \\ \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ubquodikay3x3kbcn01p.png)