Answer:
a) The time it takes the ball to reach maximum height is approximately 3.06 seconds
b) The distance of the ball from the home plate once it is at the top is approximately 38.78 m
c) No
d) The height of the ball when it is at the top is approximately 45.92 m
e) The time it takes the ball to travel 100 m horizontally is 5 seconds
F) The height of the ball when it is 100 m away from the home plate is 27.5 m
G) The height of the ball above the ground when it 100 m away from the home plate, is 27.5 m
The height of the ball above the wall at 100 m from home plate is 3.5 m
Step-by-step explanation:
The given parameters for the motion of the ball are;
The upward (vertical) velocity of the ball,
 = 30 m/s
= 30 m/s
The across (horizontal) velocity of the ball, uₓ = 20 m/s
The distance from the home plate to the outfield fence = 100 m
The height of the outfield fence = 24 m
a) The time, '
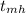 ', it takes the ball to reach maximum height is by the following kinematic equation of motion;
', it takes the ball to reach maximum height is by the following kinematic equation of motion;
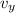 =
=
 - g·t
- g·t
Where;
 = 30 m/s
= 30 m/s
g = The acceleration due to gravity ≈ 9.8 m/s²
At maximum height, we have;
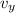 = 0 m/s, t =
= 0 m/s, t =
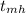
∴ 0 m/s =
 - g·
- g·
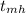
 = g·
= g·
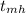
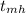 =
=
 /g
/g
∴
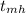 =
=
 /g = (30 m/s)/(9.8 m/s²) = 150/49 s ≈ 3.06 seconds
/g = (30 m/s)/(9.8 m/s²) = 150/49 s ≈ 3.06 seconds
The time it takes the ball to reach maximum height,
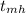 ≈ 3.06 seconds
≈ 3.06 seconds
b) The horizontal distance travelled by the ball, when it is at maximum height,
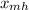 , is given as follows;
, is given as follows;
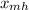 = uₓ ×
= uₓ ×
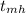 = 20 m/s × 150/49 s
= 20 m/s × 150/49 s
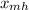 = 20 m/s × 150/49 s = 3000/49 m
= 20 m/s × 150/49 s = 3000/49 m
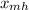 = 3000/49 m
= 3000/49 m
The distance of the ball from the home plate, 'd', once it is at the top (maximum height), is given as follows;
d = 100 m -
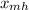
∴ d = 100 m - 3000/49 m = 1900/49 m ≈ 38.78 m
The distance of the ball from the home plate once it is at the top = d ≈ 38.78 m
c) The ball is yet to reach the fence when it gets to the top
The ball has approximately 38.78 meters to reach the fence
d) The height of the ball,
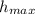 , when it is at the top is given by the following kinematic equation
, when it is at the top is given by the following kinematic equation
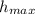 =
=
 ²/(2·g)
²/(2·g)
Where;
 = 30 m/s
= 30 m/s
g = The acceleration due to gravity ≈ 9.8 m/s²
∴
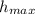 = (30 m/s)²/(2×9.8 m/s²) = 2,250/49 m ≈ 45.92 m
= (30 m/s)²/(2×9.8 m/s²) = 2,250/49 m ≈ 45.92 m
The height of the ball when it is at the top,
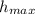 ≈ 45.92 m
≈ 45.92 m
e) The time, t₁₀₀, it will take the ball to get 100 m from home plate is found from the following relationship;
Velocity, u = Distance, x/(time, t)
∴ Time = Distance/(Velocity)
t = x/v
The given distance is the horizontal distance, therefore, we use the horizontal component of the velocity as follows;
v = Horizontal velocity of the softball = uₓ = 20 m/s
x = The given horizontal distance travelled by the ball = 100 m
t₁₀₀ = The time it takes the ball to travel 100 m horizontally
∴ t₁₀₀ = x/(uₓ) = 100 m/(20 m/s) = 5 s
The time it takes the ball to travel 100 m horizontally, t₁₀₀ = 5 seconds
F) The height of the ball above ground when it is 100 m away from the home plate is given as follows;
When the ball is 100 m from the home plate, the time, t₁₀₀ = 5 seconds
The height of the ball at 100m,
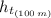 , is given according to the kinematic equation of motion for vertical height reached by an object as follows;
, is given according to the kinematic equation of motion for vertical height reached by an object as follows;
h =
 ·t - 1/2·g·t²
·t - 1/2·g·t²
∴
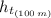 =
=
 ·t₁₀₀ - 1/2·g·t₁₀₀²
·t₁₀₀ - 1/2·g·t₁₀₀²
Plugging in the known values gives;
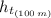 = 30 m/s × 5 s - 1/2 × 9.8 m/s × (5 s)² = 27.5 m
= 30 m/s × 5 s - 1/2 × 9.8 m/s × (5 s)² = 27.5 m
The height of the ball when it is 100 m away from the home plate,
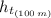 = 27.5 m.
= 27.5 m.
G) The height of the ball above the ground when it 100 m away from the home plate, is
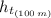 = 27.5 m
= 27.5 m
The height of the ball above the wall at 100 m from the home plate = The height of the ball when it is 100 m away from the home plate - The height of the wall at 100 m away from the home plate
∴ The height of the ball above the wall at 100 m from home plate = 27.5 m - 24 m = 3.5 m.