Question

How would I graph f and g ?f (x) = | x - 4|g (x) = |3x - 4|

Answer 1

The given function

`f(x)=|x-4|`

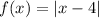
Represents a function for the absolute value of x, this indicates that the function is V shaped.

To graph it you have to determine at least three points: The vertex and one point for each arm of the function.

The coefficient that multiplies the absolute value is positive a=+1, this indicates that the V will open upwards.

The function is written in vertex form, if you remember the structure of this form:

`f(x)=a|x-h|+k`

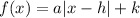
Where

h is the x-coordinate of the vertex → in the formula it always appears with the opposite sign. If you see it +, then the coordinate is negative and vice versa.

k is the y-coordinate of the vertex

For our function

`f(x)=|x-4|`

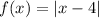
The value inside the absolute term is the x-coordinate of the vertex: h=+4

There is no value outside the absolute term, this indicates that the y-coordinate of the vertex is zero: k=0

Vertex: (4, 0)

Now we have to determine one point for the left arm of the function and one value for the right arm of the function.

Since the vertex is at x=4, I'll use x=2 for the left point and x=6 for the right point

Left point

Replace the formula with x=2

`\begin{gathered} f(x)=|x-4| \\ f(2)=|2-4| \\ f(2)=|-2| \\ f(2)=2 \end{gathered}`

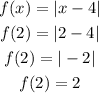
The left point is (2, 2)

Right point

Replace the formula with x=6

`\begin{gathered} f(x)=|x-4| \\ f(6)=|6-4| \\ f(6)=|2| \\ f(6)=2 \end{gathered}`

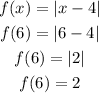
The right point is (6, 2)

Now using the three points you can plot the function.