Question

A store sells two different types of coffee beans; the more expensive one sells for $8 per pound, and the cheaper one sells for $4 per pound. The beans

are mixed to provide a mixture of 50 pounds that sells for $6.50 per pound. How much of each type of coffee bean should be used to create 50 pounds of the mixture?

Answer 1

So,

Let the amount of the expensive coffee beans be x, and the amount of the less expensive coffee bean be y.

The number of pounds of coffee beans is 50.
x + y = 50

$8 times the amount of more expensive coffee beans plus $4 times the amount of less expensive coffee beans divided by 50 equals $6.50.

`(8x + 4y)/(50) = 6.50`

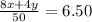
Now, all we have to do is use Elimination by Substitution.
x + y = 50

Subtract y from both sides.
x = 50 - y

Substitute 50 - y for x in the second equation.

`(8(50 - y) + 4y)/(50) = 6.50`

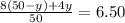
Distribute.

`(400 - 8y + 4y)/(50) = 6.50`

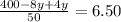
Collect Like Terms.

`(400 -4y)/(50) = 6.50`

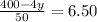
Simplify.

`(4(100 -y))/(2*5^2) = 6.50`

`(2(100 -y))/(5^2) = 6.50`

`(200 - 2y)/(25) = 6.50`

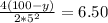
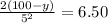
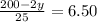
Multiply both sides by 25.

`200 - 2y = 162.5`

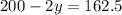
Add 2y to both sides.

`200 = 162.5 + 2y`

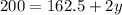
Subtract 162.5 from both sides.
37.5 = 2y

Divide both sides by 2.
18.75 = y

Substitute in an earlier equation to solve for x.
x = 50 - y
x = 50 - 18.75
x = 31.25

Check.
31.25 + 18.75 = 50 lbs.


`(8x + 4y)/(50) = 6.50`

`(8(31.25) + 4(18.75))/(50) = 6.50`

`(250 + 75)/(50) = 6.50`

`(325)/(50) = 6.50`

`(5^2*13)/(2 * 5^2) = 6.50`

`(13)/(2) = 6.50`
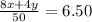
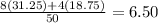
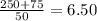
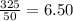
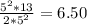
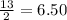
6.50 = 6.50 This also checks.

There were 31.75 pounds of the more expensive coffee bean and 18.75 pounds of the less expensive coffee bean.