Question

(n+1)!-------(n-1)! the choices are (n+1)(n)(n-1), (n+2)(n+1)(n), (n), and (n+1)(n)

Answer 1

not sure,,

Explanation:

Answer 2

To answer this question, we need to remember the nature of the factorial of a number. It can be expressed as:

`n!=n\cdot(n-1)\cdot(n-2_{})\cdot3\cdot2\cdot1`

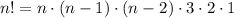
We can use the same principle to simplify the expression in the question, as follows:

`((n+1)!)/((n-1)!)=((n+1)\cdot(n+1-1)\cdot(n+1-2)!)/((n-1)!)`

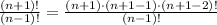
Now, we have:

`((n+1)!)/((n-1)!)=((n+1)\cdot(n)\cdot(n-1)!)/((n-1)!)`

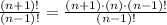
Since we have that:

`((n-1)!)/((n-1)!)=1`

The expression can be written as:

`((n+1)!)/((n-1)!)=(n+1)\cdot n`

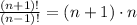
Therefore, the original equation can be rewritten as (n+1) * n (last option).