Question

16.) Suppose the one side of a right triangle is 3 cm more than theshortest side. Suppose the hypothenuse is 3 cm less than twice theshortest side. Set up and solve an equation to find the three sides ofthe right triangle. Pythagorean Theorem(11 pts)

Answer 1

Step 1 :

In this question, we are told that the one side of a right triangle is 3 cm more than the shortest side.

Suppose the hypothenuse is 3 cm less than twice the shortest side.

Step 2 :

The diagram is as shown below:

Step 3 :

Using the Pythagorean Theorem, we have that:

`(x+3)^2+x^2=(2x-3)^2`
`\begin{gathered} x^2+6x+9+x^2=4x^2\text{ - 12 x + 9} \\ 2x^2+6x+9=4x^2\text{ -12 x + 9} \\ \text{collect like terms, we have that:} \end{gathered}`
`\begin{gathered} 4x^2-2x^2-12\text{ x - 6 x +9 -9 = 0} \\ 2x^2\text{ - 18x = 0} \\ 2\text{ x ( x - 9 ) = 0} \\ \text{x = 0 or x = 9 ( we ignore x = 0 ) } \end{gathered}`

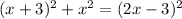
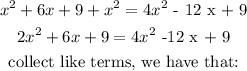
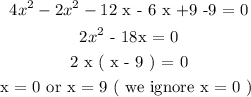
Step 4 :

The lengths of the triangle are as follows:

`\begin{gathered} \text{x = 9} \\ \text{x + 3 = 9 + 3 = 12 } \\ 2\text{ x - 3 = 2(9 ) - 3 = 18 - 3 = 15} \end{gathered}`

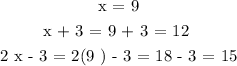
CONCLUSION:

The three sides of the triangle are 9 cm, 12 cm and 15 cm.