Question

Suppose 30 blackberry plants started growing in a yard. Absent constraint, the blackberry plants will spread by 100% a month. If the yard can only sustain 60 plants, use a logistic growth model to estimate the number of plants after 3 months.

Answer 1

Answer:

The number of plants in the yard after 3 months = 60

Step-by-step explanation:

The number of blackberry plants that started growing in the yard, p₀ = 30

The blackberry plants will spread by 100% a month

p(1) = 30 + 1(30)

p(1) = 60

The yard can only sustain 60 plants, m = 60

The logistic growth model is given as:

`p=(m)/(1+((m)/(p_0)-1)e^(-rt))`

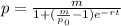
Substitute p₀ = 30, p = 60, t = 1, and m = 60 to solve for the growth rate, r.

`\begin{gathered} 60=(60)/(1+((60)/(30)-1)e^(-r(1))) \\ 60=(60)/(1+(2-1)e^(-r)) \\ 60=(60)/(1+e^(-r)) \\ 60(1+e^(-r))=60 \\ 1+e^(-r)=(60)/(60) \\ e^(-r)=1-1 \\ e^(-r)=0 \\ \ln (e^(-r))=\ln 0 \\ -r=-\infty \\ r=\infty \end{gathered}`

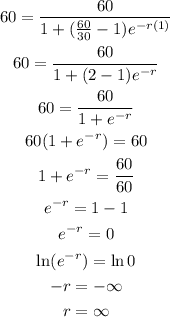
To estimate the number of plants after 3 months:

substitute t = 3, and r = ∞ into the logistic model

`\begin{gathered} p=(m)/(1+((m)/(p_0)-1)e^(-rt)) \\ p(3)=(60)/(1+((60)/(30)-1)e^(-\infty(3))) \\ p(3)=(60)/(1+e^(-\infty)) \\ p(3)=(60)/(1+0) \\ p(3)=(60)/(1) \\ p(3)=60 \end{gathered}`

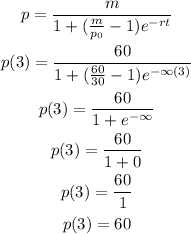
The number of plants in the yard after 3 months = 60