Question

To approximate the length of the pond, you walk 200 ft from point A to point B, turn 80 degrees and walk 160 ft to point C. Approximate the length AC of the pond. Round your answer to 2 decimal points.

Answer 1

276.97 ft

Step-by-step explanation:

We can represent the situation with the following diagram

Now, to find the distance from A to C, we first need to find the measure of angle B, so

∠B = 180 - 80

∠B = 100

Then, using the cosine law, we can find the distance from A to C as follows

`AC^2=(AB)^2+(BC)^2-2(AB)(BC)\cos (100)`

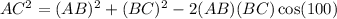
Replacing the values and solving for AC, we get:

`\begin{gathered} AC^2=(200)^2+(160)^2-2(200)(160)\cos (100) \\ AC^2=76713.48 \\ AC=\sqrt[]{76713.48} \\ AC=276.97\text{ ft} \end{gathered}`

Therefore, the answer is 276.97 ft