Question

Verify identity list steps. Cot(t)(1-cos^2(t))=cos(t)sin(t)

Answer 1

Remember: We have to work from either the LHS or the RHS.
(Left hand side or the Right hand side)

You should already know this:


`\huge{Cot(t) = (1)/(tan(t)) = (1)/((sin(t))/(cos(t))) = 1/ (sin(t))/(cos(t)) = 1* (cos(t))/(sin(t))=\boxed{(cos(t))/(sin(t))}`


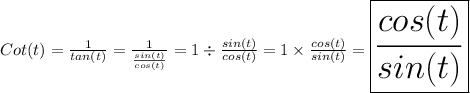
You should also know this:


`sin^2(t) + cos^2(t) = 1\\\\\boxed{sin^2(t)} = 1 - cos^2(t)`

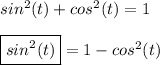
So plugging in both of those into our identity, we get:


`(cos(t))/(sin(t))\cdot sin^2(t) = cos(t)\cdot sin(t)`

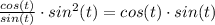
Simplify the denominator on the LHS (Left Hand Side)

We get:


`cos(t) \cdot sin(t) = cos(t) \cdot sin(t)`

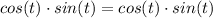
LHS = RHS

Therefore, identity is verified.