Question

The area of a triangle abc is 4√2 m²

Answer 1

x = 3.08

Explanation:

Construct a perpendicular AD from point A to opposite side BC,

By sine ratio,

sin(45)° =
`\frac{\text{Opposite side}}{\text{Hypotenuse}}`

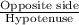
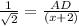
`(1)/(√(2))= (AD)/((x+2))`

AD =
`(x+2)/(√(2))`

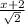
Area of a triangle =
`(1)/(2)(\text{Base})(\text{Height})`

=
`(1)/(2)(BC)(AD)`

`4√(2)=(1)/(2)(2x-3)((x+2))/(√(2) )`

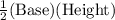
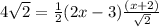
(2x - 3)(x + 2) = 16

2x(x + 2) - 3(x + 2) = 16

2x² + 4x - 3x - 6 = 16

2x² + x - 6 = 16

2x² + x - 22 = 0

By using quadratic formula,

x =
`\frac{-1\pm\sqrt{(1)^(2)-4(2)(-22)}}{2(2)}`

x =
`(-1\pm√(177))/(4)`

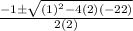
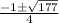
x = 3.076, -3.576

x ≈ 3.08, -3.58

But length of the sides can't be negative

Therefore, x = 3.08 will be the answer.