we know that
It is much easier to compute the number of numbers that do not contain a
 .
.
In the first
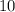 numbers
numbers
 do not contain a
do not contain a
 .
.
In the first
 numbers
numbers
 do not contain a
do not contain a
 . (This is because these numbers are formed by selecting a digit out of
. (This is because these numbers are formed by selecting a digit out of
![[0, 1, 2, 4, 5, 6, 7, 8, 9]](https://img.qammunity.org/2015/formulas/mathematics/high-school/mdhw158r8q9sp0z32ehagrpps59szlv77o.png) for the first position and another digit out of the same set for the last position and this may be done in
for the first position and another digit out of the same set for the last position and this may be done in

In the first
 numbers, reasoning as above, there are
numbers, reasoning as above, there are
 numbers that do not contain a
numbers that do not contain a
 .
.
Now the pattern should be becoming obvious.
In the first
 numbers there are
numbers there are
 numbers that do not contain a
numbers that do not contain a
 .
.
So
In the first
 numbers there are
numbers there are
 numbers that do not contain a
numbers that do not contain a
 .
.


Thus
the ratio of those numbers that do contain a 3 over the total is equal to

therefore
the answer is
