Question

Scott invested a total of $5400 at two separate banks. One bank pays simple interest of 10% per year while the other pays simple interest at a rate of 8% per year. If Scott eamed $492.00 in interest during asingle year, how much did he have on deposit in each bank?

Answer 1

Given:

Total principal = $5400

Interest rate of bank A = 10% = 0.10

Interest rate of bank B = 8% = 0.08

Total interest = $492

Let's find how much he deposited in each bank.

Equation for total principal:

A + B = 5400

Equation for total interest:

0.10A + 0.08B = 492

Hence, we have the system of equations:

A + B = 5400

0.10A + 0.08B = 492

Where A and B represents the amount deposited in each bank.

Let's solve the system simultaneously using substitution method:.

Rewrite the first equation for A:

A = 5400 - B

Substitute (5400 - B) for A in equation 2:

`\begin{gathered} 0.10(5400-B)+0.08B=492 \\ \\ 540-0.1B+0.08B=492 \\ \\ -0.1B+0.08B=492-540 \\ \\ -0.02B=-48 \end{gathered}`

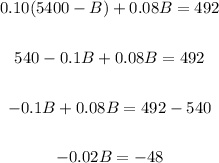
Divide both sides by -0.02:

`\begin{gathered} (-0.02B)/(-0.02)=(-48)/(-0.02) \\ \\ B=2400 \end{gathered}`

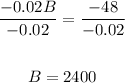
Now, substitute 2400 for B in either of the equations:

`\begin{gathered} A=5400-B \\ \\ A=5400-2400 \\ \\ A=3000 \end{gathered}`

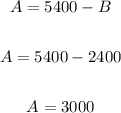
Therefore, we have the following:

Amount deposited in the bank that pays 10% interest = $3000

Amount deposited in the bank that pays 8% interest = $2400

• ANSWER:

Amount deposited in the bank that pays 10% interest = $3000

Amount deposited in the bank that pays 8% interest = $2400