Question

Can anyone help me?pls

Answer 1

b = 8.89, c = 11.96 and m∠B = 48°

Explanation:

From the given triangle ABC,

We will apply sine ratio for angle A,

sin(A) =
`\frac{\text{Opposite side}}{\text{Hypotenuse}}`

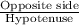
sin(42)° =
`(BC)/(AB)`

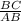
sin(42)° =
`(8)/(AB)`

AB =
`\frac{8}{\text{sin}(42)}`

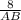
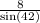
AB = 11.96

c = 11.96

By triangle sum theorem,

m∠A + m∠B + m∠C = 180°

42° + m∠B + 90° = 180°

m∠B = 180 - 132

m∠B = 48°

By cosine ratio of angle A,

cos(A) =
`\frac{\text{Adjacent side}}{\text{Hypotenuse}}`

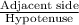
cos(42)° =
`(AC)/(AB)`

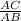
AC = AB.cos(42)°

AC = (11.96)cos(42)°

AC = 8.89

b = 8.89