Answer:
1. The impulse of the force is 4.62 kg·m/s
2. A. The negative velocity is the return 10 m/s velocity on the way upwards
B. The initial momentum of the object is 576 kg·m/s
C. The final momentum of the object is -480 kg·m/s
D. The change of momentum of the object is -1,056 kg·m/s
Step-by-step explanation:
1. The magnitude of the applied force, F = 14 N
The duration of the applied force, Δt = 0.33 seconds
The impulse of the force, I = F × Δt
By substitution of the values, we have;
The impulse of the force, I = 14 N × 0.33 s = 4.62 N·s = 4.62 kg·m/s
2. The mass of the object, m = 48 kg
The initial velocity of the object, v₁ = 12 m/s
The final velocity of the object, v₂ = -10 m/s
A. The initial velocity = 12 m/s (downwards)
The negative velocity is the velocity that is in the opposite direction to the initial downward velocity, therefore, the upwards 10 m/s velocity is the negative velocity
B. The initial momentum of the object,
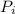 = m₁·v₁
= m₁·v₁
By substituting the values, we have;
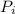 = 48 kg × 12 m/s = 576 kg·m/s
= 48 kg × 12 m/s = 576 kg·m/s
C. The final momentum of the object,
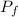 = m₂·v₂
= m₂·v₂
By substituting the values, we have;
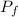 = 48 kg × (-10 m/s) = -480 kg·m/s
= 48 kg × (-10 m/s) = -480 kg·m/s
D. The change of momentum of the object, ΔP =
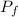 -
-
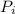
∴ ΔP = -480 kg·m/s - 576 kg·m/s = -1,056 kg·m/s
The change of momentum of the object, ΔP = -1,056 kg·m/s.