Question

The sides of a square are 3 cm long. One vertex of the

square is at (2,0) on a square coordinate grid marked in
centimeter units. Which of the following points could
also be a vertex of the square?
F. (−4, 0)
G. ( 0, 1)
H. ( 1,−1)
J. ( 4, 1)
K. ( 5, 0)

Answer 1

K (5.0) It's easy just use 2plus3and that's it.

Answer 2

Answer: The required point that could also be a vertex of the square is K(5, 0).

Step-by-step explanation: Given that the sides of a square are 3 cm long and one vertex of the square is at (2,0) on a square coordinate grid marked in centimeter units.

We are to select the co-ordinates of the point that could also be a vertex of the square.

To be a vertex of the given square, the distance between the point and the vertex at (2, 0) must be 3 cm.

Now, we will be suing the distance formula to calculate the lengths of the segment from the point to the vertex (2, 0).

If the point is F(-4, 0), then the length of the line segment will be

`\ell=√((-4-2)^2+(0-0)^2)=√(6^2+0^2)=√(6^2)=6~\textup{cm}\\eq 3~\textup{cm}.`

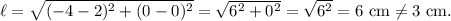
If the point is G(0, 1), then the length of the line segment will be

`\ell=√((0-2)^2+(1-0)^2)=√(2^2+1^2)=√(4+1)=\sqrt5~\textup{cm}\\eq 3~\textup{cm}.`

If the point is H(1, -1), then the length of the line segment will be

`\ell=√((1-2)^2+(-1-0)^2)=√(1^2+1^2)=√(1+1)=\sqrt2~\textup{cm}\\eq 3~\textup{cm}.`

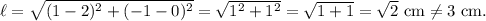
If the point is J(4, 1), then the length of the line segment will be

`\ell=√((4-2)^2+(1-0)^2)=√(2^2+1^2)=√(4+1)=\sqrt5~\textup{cm}\\eq 3~\textup{cm}.`

If the point is K(5, 0), then the length of the line segment will be

`\ell=√((5-2)^2+(0-0)^2)=√(3^2+0^2)=√(3^2)=3~\textup{cm}.`

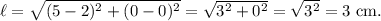
Thus, the required point that could also be a vertex of the square is K(5, 0).