Question

Determine if JK and LM are parallel, perpendicular, or neither. J(1, 9), K(7, 4), L(8, 13), M(-2, 1).

Answer 1

First of all, we need to remember two statements:

1) two lines are perpendicular when the product of its slopes is equal to -1.

2) two lines are parallel when they have the same slope.

Now, we need to find the slope for both lines, we start with the segment of line JK

`\begin{gathered} m=\text{slope}=((y_2-y_1))/((x_2-x_1));\text{ } \\ J(1,9)=J(x_1,y_1);x_1=1;y_1=9 \\ K(7,4)=J(x_2,y_2);x_2=7;y_2=4 \\ m=\text{slope}=((y_2-y_1))/((x_2-x_1))=((4-9))/((7-1))=(-5)/(6) \\ m=(-5)/(6) \end{gathered}`

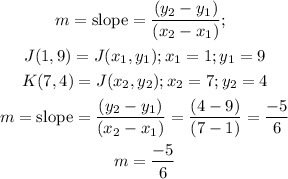
In the same way, we need to find the value of the slope to the segment LM

`\begin{gathered} m=\text{slope}=((y_2-y_1))/((x_2-x_1)); \\ L(8,13)=L(x_1,y_1);x_1=8;y_1=13 \\ M(-2,1)=M(x_2,y_2);x_2=-2;y_2=1 \\ m=\text{slope}=((y_2-y_1))/((x_2-x_1))=((1-13))/((-2-8))=(-12)/(-10)=(6)/(5) \\ m=(6)/(5) \end{gathered}`

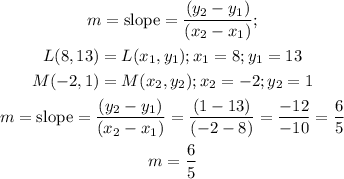
From that we can conclude that both segments are NOT parallel,

Now, we verify if they are perpendicular multiplying the slopes, like this:

`(-5)/(6).(6)/(5)=-1`

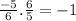
Finally, we conclude that both segments are parallel because the product of its slopes are -1.