Continuity of Functions
Continuity is a property of functions that can be drawn without lifting the pencil off the paper/board.
A function that is not continuous at a given point x=a is said to be discontinuous at x=a.
There are 3 types of discontinuity: Removable, Jump, and Infinite.
We'll select the appropriate type and explain it when we are required to.
The given function is:
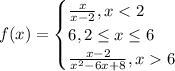
Rational functions provide discontinuity points and piecewise functions need to be analyzed to check the continuity in their endpoints.
The denominator of the first piece is x-2 which gives us one possible point of discontinuity at x=2, which also happens to be an endpoint of the first two pieces of the function, thus x=2 needs to be analyzed.
The other point is x=6 since the function changes from the second to the third piece.
Finally, the denominator of the last piece has two possible zeros at x=2 and x=4. Since both points lie out of the interval x>6, they don't need to be considered.
Thus, the only points of possible discontinuity are x=2 and x=6. Let's analyze them.
The left-side limit at x=2 does not exist because it makes the denominator zero and the function is undefined, i.e., the limit tends to be infinite.
This discontinuity is, therefore, of the type infinite.
The left-side limit at x=6