Question

A car and a lorry are about to collide. When they collide the two vehicles become tightly locked together. The lorry is going at a speed of 20km/h and weighs 9.5 tonnes. The car is going at a speed of 40km/h and is 0.5 tonnes. Calculate the speed of the vehicles immediately after the collision. (6 marks)

Answer 1

The speed of the vehicles immediately after the collision is 5.84 m/s.

Step-by-step explanation:

The speed of the vehicles after the collision can be found by conservation of linear momentum:

`p_(i) = p_(f)`

`m_(1)v_{1_(i)} + m_(2)v_{2_(i)} = m_(1)v_{1_(f)} + m_(2)v_{2_(f)}`

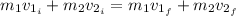
Where:

m₁: is the mass of the car = 0.5 ton = 500 kg

m₂: is the mass of the lorry = 9.5 ton = 9500 kg

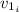`v_{1_(i)}`: is the initial speed of the car = 40 km/h = 11.11 m/s

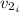`v_{2_(i)}`: is the initial speed of the lorry = 20 km/h = 5.56 m/s

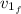`v_{1_(f)}`: is the final speed of the car =?

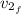`v_{2_(f)}`: is the final speed of the lorry =?

Since the two vehicles become tightly locked together after the collision
`v_{1_(f)}` =
`v_{2_(f)}`:

`m_(1)v_{1_(i)} + m_(2)v_{2_(i)} = v(m_(1) + m_(2))`

`v = \frac{m_(1)v_{1_(i)} + m_(2)v_{2_(i)}}{m_(1) + m_(2)} = (500 kg*11.11 m/s + 9500 kg*5.56 m/s)/(500 kg + 9500 kg) = 5.84 m/s`

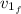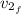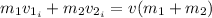
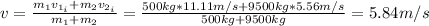
Therefore, the speed of the vehicles immediately after the collision is 5.84 m/s.

I hope it helps you!