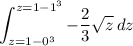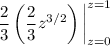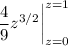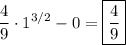Question

Determine the area of the shaded region bounded by the implicitly defined curve

x^2 = y^4( 1 - y^3 )

Answer 1

Suppose x ≥ 0. Then

x² = y⁴ (1 - y³) ⇒ x = √(y⁴ (1 - y³)) = y² √(1 - y³)

On the other hand, if x < 0, then

x² = y⁴ (1 - y³) ⇒ x = - y² √(1 - y³)

Either expression for x in terms of y describes half of the curve, to either side of the y-axis (i.e. the line x = 0).

Find where these two curves intersect:

y² √(1 - y³) = - y² √(1 - y³)

2y² √(1 - y³) = 0

2y² = 0 or √(1 - y³) = 0

y = 0 or 1 - y³ = 0

y = 0 or y³ = 1

y = 0 or y = 1

So, the two halves meet at the points (0, 0) and (0, 1).

The area between the halves is then given by the integral

`\displaystyle \int_(y=0)^(y=1) \left(y^2√(1-y^3) - \left(-y^2√(1-y^3)\right)\right) \, dy`

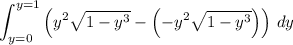
Let's calculate it:

`\displaystyle \int_(y=0)^(y=1) 2y^2 √(1-y^3) \, dy`

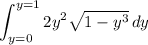
Substitute z = 1 - y³ and dz = -3y² dy.

`\displaystyle \int_(z = 1 - 0^3)^(z = 1 - 1^3) -\frac23 √(z) \, dz`

`\displaystyle -\frac23 \int_(z = 1)^(z = 0) √(z) \, dz`

`\displaystyle \frac23 \int_(z = 0)^(z = 1) z^(1/2) \, dz`

`\displaystyle \frac23 \left(\frac23 z^(3/2)\right) \bigg|_(z=0)^(z=1)`

`\displaystyle \frac49 z^(3/2) \bigg|_(z=0)^(z=1)`

`\displaystyle \frac49 \cdot 1^(3/2) - 0 = \boxed{\frac49}`