Answer:
Step 4
Step-by-step explanation:
The initial system of equation is:
5x + 4y = 1
4x + 2y = 8
So, if we take the second equation and isolate y, we get:
y = 4 - 2x
Then, replacing it on the first one, we get:
5x + 4(4 - 2x) = 1
Solving for x, we get:
5x + 4*4 - 4*2x = 1
5x + 16 - 8x = 1
-3x +16 = 1
-3x + 16 - 16 = 1 - 16
-3x = -15
Finally, dividing by -3, we get:
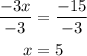
Therefore, the mistake was made in step 4, because he didn't take into account the negative sign. So, the correct answer is x = 5 instead of x = - 5