To answer this question, the first step we have to follow is to set 3 equations for the 3 triangles according to the pythagorean theorem:
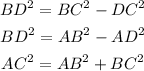
From this, we can use the first two equations and make them equal:
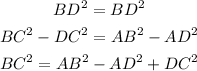
Now, we can use the expression for BC and replace it in the third equation:
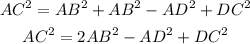
Replace for the known values and solve for AB^2 (remember that AC=AD+DC):

Using this value of AB^2 and the value of AD, we can use the second equation to find BD:
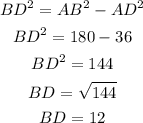
It means that BD has a measure of 12.
The correct answer is a. 12.