Question

From the triangle below, if AD = 6 and CD = 24, find the length of side BD.

Answer 1

To answer this question, the first step we have to follow is to set 3 equations for the 3 triangles according to the pythagorean theorem:

`\begin{gathered} BD^2=BC^2-DC^2 \\ BD^2=AB^2-AD^2 \\ AC^2=AB^2+BC^2 \end{gathered}`

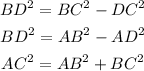
From this, we can use the first two equations and make them equal:

`\begin{gathered} BD^2=BD^2 \\ BC^2-DC^2=AB^2-AD^2 \\ BC^2=AB^2-AD^2+DC^2 \end{gathered}`

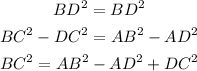
Now, we can use the expression for BC and replace it in the third equation:

`\begin{gathered} AC^2=AB^2+AB^2-AD^2+DC^2 \\ AC^2=2AB^2-AD^2+DC^2 \end{gathered}`

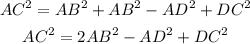
Replace for the known values and solve for AB^2 (remember that AC=AD+DC):

`\begin{gathered} 30^2=2AB^2-6^2+24^2 \\ 900=2AB^2-36+576 \\ 900=2AB^2+540 \\ 2AB^2=360 \\ AB^2=180 \end{gathered}`

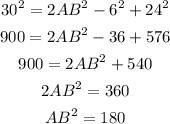
Using this value of AB^2 and the value of AD, we can use the second equation to find BD:

`\begin{gathered} BD^2=AB^2-AD^2 \\ BD^2=180-36 \\ BD^2=144 \\ BD=√(144) \\ BD=12 \end{gathered}`

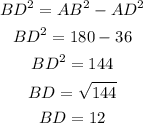
It means that BD has a measure of 12.

The correct answer is a. 12.