Question

"the guidelines of the section" this means to graph and then state where the inflection points, critical points, concave up and down points, etc are#36

Answer 1

Given:

The function

`f(x)=ln(x^2+1)`

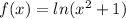
Required:

State where the inflection points, critical points, concave up and down points.

Step-by-step explanation:

Inflection points are points where the function changes concavity, i.e. from being "concave up" to being "concave down" or vice versa.

A graph is said to be concave up at a point if the tangent line to the graph at that point lies below the graph in the vicinity of the point and concave down at a point if the tangent line lies above the graph in the vicinity of the point.

A critical point is a point in the domain of the function where the function is either not differentiable or the derivative is equal to zero.

The graph is

Now,

`\begin{gathered} \text{ Inflection points }=(-1,ln2),(1,ln2) \\ \text{ Critical points }=(0,0) \\ \text{ Concave upward on }(-1,1) \\ \text{ Concave downward on }(-\infty,-1)\cup(1,\infty) \end{gathered}`

Answer:

answered the question.