Question

Please help ! i need help with my geometry homework

Answer 1

x = 9

Explanation:

We have three right triangles

For the biggest one from Pythagoras Theorem the square of its base side length (let it be a) is:

a² = (x+7)² - 12²

The square of the segment inside the biggest triangle (let it be h) is:

From the smallest triangle: h² = a² - 7²

From the medium triangle: h² = 12² - x²

Therefore:

a² - 7² = 12² - x²

(x+7)² - 12² - 7² = 12² - x²

x² + 2·x·7 + 7² - 12² - 7² = 12² - x²

x² + 14x - 144 = 144 - x²

x² + x² + 14x -144 - 144 = 0

2x² + 14x - 288 = 0

x² + 7x - 144 = 0

`a=1\,,\ b=7\,,\ c=-144\\\\\bold{x=(-7\pm√(7^2-4\cdot1\cdot(-144)))/(2\cdot1)=(-7\pm√(49+576))/(2)=\frac{-7\pm√(625)}2}`

`\bold{x=(-7+25)/(2)=9}`

{
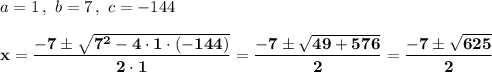
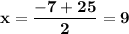
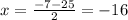`x=(-7-25)/(2)=-16` <0, so is not apllicable}