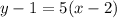Answer:
The equation of the line is:
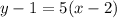
Explanation:
Given
Pass through
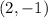
Parallel to:
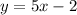
Required
Determine the equation in point slope form
An equation has a general form:
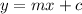
Where:
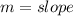
Compare:
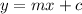 to
to
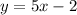
we have:
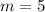
Since the line is parallel to
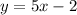 , then they have the same slope of 5
, then they have the same slope of 5
The line equation is then calculated using:
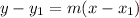
Where
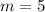
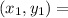
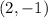
So, we have: