Question

Graph x+3y<(or equal to)6, indicating the solution set with cross hatching or shading. Explain how you determine where to draw the line and shade the area that represents the solution set.

Answer 1

Step 1

Given;

`x+3y\leq6`

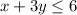
Required; To graph the inequality

Step 2

Graph the function

`\begin{gathered} We\text{ find the y-intercept by setting x=0} \\ 0+3y\leq6 \\ y\leq2 \\ First\text{ point\lparen0,2\rparen} \end{gathered}`
`\begin{gathered} We\text{ find the x-intercept by setting y=0} \\ x+3(0)\leq6 \\ x\leq6 \\ Secon\text{d point;\lparen6,0\rparen} \end{gathered}`

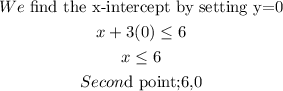
So by finding the x-intercept and y-intercept, we can determine where to draw the line. Since the inequality is greater than or equal to the line will be continuous and not broken. Also, we will know the area we will shade by;

`\begin{gathered} Resolving\text{ the inequality and make y the subject of the formular} \\ x+3y\leq6 \\ 3y\leq6-x \\ y\leq2-(x)/(3) \end{gathered}`

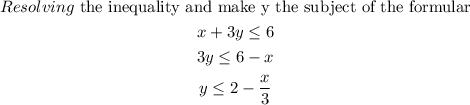
Since if we set x=0, we get y < or equal to 2, then we know that the shaded area will be where y is equal to and below. There we will shade below the point (0,2) to represent the solution set.