For the given question, we will find the equation of the parabola of each box
then, we will select the correct equation from the tiles
The first box: focus (2, -2) and directrix y = -8
So, the parabola will open up and the equation will be:

simplify the equation

The second box: Focus (-3, 6) and Directrix (x = -11)
So, the parabola will open right
The values of (a) and the vertex (h,k) will be:

The equation of the parabola will be:
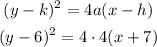
Simplifying the equation:

The third box: Focus (2, -2); Directrix (x = 8)
So, the parabola will open left
The values of (a) and the vertex (h,k) will be:
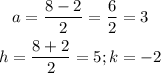
The equation of the parabola will be:
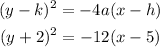
Simplifying the equation:
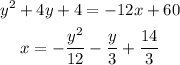
The fourth box: Focus (-7, 1) and Directrix (y = 11)
The parabola will open down
The values of (a) and the vertex (h,k) will be:
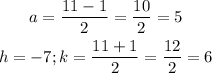
The equation of the parabola will be:
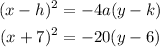
Simplifying the equation:

The drag of the tiles to the boxes according to the following figure: