Given:
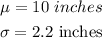
To find- P(X>15)
Explanation-
We know that a z-score is given by-
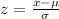
where x is the raw score, mu is the mean and sigma is the standard deviation.
Hence, the proportion of trees having a diameter greater than 15 inches will be-
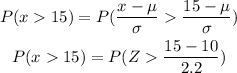
On further solving, we get
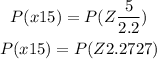
With the help of an online tool, the probability will be
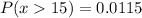
Since the significance level is not mentioned, we assumed it is 0.05.
Thus, the proportion of trees having a diameter greater than 15 inches is 0.0115.
The answer is 0.0115.