Question

Maple tree diameters in a forest area are normally distributed with mean 10 inches and standard deviation 2.2 inches. Find the proportion of trees having a diameter greater than 15 inches.

Answer 1

Given:

`\begin{gathered} \mu=10\text{ }inches \\ \sigma=2.2\text{ inches} \end{gathered}`

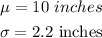
To find- P(X>15)

Explanation-

We know that a z-score is given by-

`z=(x-\mu)/(\sigma)`

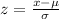
where x is the raw score, mu is the mean and sigma is the standard deviation.

Hence, the proportion of trees having a diameter greater than 15 inches will be-

`\begin{gathered} P(x>15)=P((x-\mu)/(\sigma)>(15-\mu)/(\sigma)) \\ P(x>15)=P(Z>(15-10)/(2.2)) \end{gathered}`

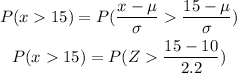
On further solving, we get

`\begin{gathered} P(x\gt15)=P(Z\gt(5)/(2.2)) \\ P(x\gt15)=P(Z\gt2.2727) \end{gathered}`

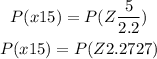
With the help of an online tool, the probability will be

`P(x>15)=0.0115`

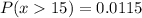
Since the significance level is not mentioned, we assumed it is 0.05.

Thus, the proportion of trees having a diameter greater than 15 inches is 0.0115.

The answer is 0.0115.