Question

The widths of two similar rectangles are 16 cm and 14 cm. What is the ratio of their perimeters? Of their areas?

a.
8:7 and 64:49
b.
9:8 and 64:49
c.
8 and 81-64
d.
8:7 and 81:64

Answer 1

`(16)/(14)=(8)/(7)=8:7-ratio\ of\ perimeters\\\\8^2:7^2=64:49-ratio\ of\ areas\\\\Answer:A.`

Answer 2

A

Explanation:

Two lengths of similar figures relates by the scale factor
`k`.

Two areas of similar figures relates by the scale factor
`k^(2)`.

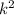• If length of one figure is A, and corresponding length of another figure is B, then they are related by:

`A=kB`

• If area of one figure is A, and corresponding Area of another figure is B, then they are related by:

`A=k^(2)B`

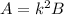
So we can write:

`16=k(14)\\k=(16)/(14)=(8)/(7)`

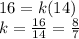
Since, perimeter is also length, the ratio would be
`(8)/(7)`

Similarly, ratio of their areas should be
`(8^2)/(7^2)=(64)/(49)`

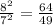
Answer choice A is right.