SOLUTION
Given the question in the tab, the following are the solution steps to answer the question.
STEP 1: Write the given data

STEP 2: Write the formula for the are of a triangle
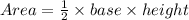
STEP 3: Substitute the given values

STEP 4: Cross multiply
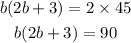
Open the bracket
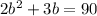
Subtract 90 from both sides
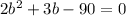
STEP 5: Solve the derived equations using quadratic formula
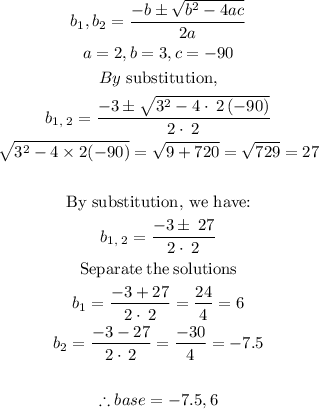
Since the value of the base of a triangle can not be negative, the base of the triangle is 6ft
STEP 6: Find the value of the height
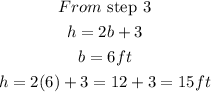
Hence, the dimension of the triangle are:
base = 6ft
height = 15ft