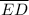Question

In the figure, E is the midpoint of AB and CD, and AB =CD. Write a paragraph proof to prove that AE = ED.Given:Prove:Proof:

Answer 1

A two-column proof to prove that segment AE is congruent with segment ED should be completed as follows;

Statements Reasons_______

1. E is the midpoint of AB and CD 1. Given

AB = CD

2. AE = AB/2, ED = CD/2 2. Midpoint Theorem

3. AB/2 = CD/2 3. Multiplication property of equality

4. AE = ED 4. Substitution property

5.
`\overline_AE` ≅
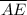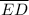`\overline_ED` 5. Definition of congruent segments.

In Mathematics, the Midpoint Theorem states that a point lies exactly at the middle of two other end points which are located on a straight line segment, provided it is equidistant from both end points.

Since point E is the midpoint of segment AB, AE is congruent to EB based on the Midpoint Theorem, similarly CE is congruent to ED. By the definition of congruent segments, AE = EB = AB/2, and CE = ED = CD/2.

Since AB = CD, we know that AB/2 = CD/2 based on the multiplication property of equality. In this context, AE must be equal to ED. Therefore, segment AE is congruent to segment ED by the definition of congruent segments;

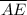`\overline_AE` ≅
`\overline_ED`

Answer 2

Given:

E is the midpoint of AB

E is the mispoint of CD

AB=CD

Prove:

AE = ED

Proof:

If E is midpoint of AB, then AE=AB/2.

If E is midpoint of CD, then ED=CD/2.

If AB=CD, then

AE=AB/2=CD/2=ED