Question

PLEASE HELP !
3⋅f(−4)−3⋅g(−2) ???

Answer 1

Answer: −12f+6g

Explanation:

Answer 2

The expression
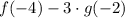`\(f(-4) - 3 \cdot g(-2)\)` is evaluated using the given functions' graphs. Substituting the corresponding values yields
`\(f(-4) - 3 \cdot g(-2) = -12\).`

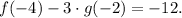
To find f(−4)−3⋅g(−2), we look at the given values in the functions' graphs. For f(−4), we find that the corresponding y-value is -3. For g(−2), the corresponding y-value is 3. Substituting these values into the expression:

`\[ f(-4)-3.g(-2) = (-3) - 3 \cdot 3 = -3 - 9 = -12 \]`

Therefore, f(−4)−3⋅g(−2) = -12. The graph values indicate that at x = -4 in function f, the y-value is -3, and at x = -2 in function g, the y-value is 3. Subtracting three times the g value from the f value gives -12.