Question

A 900 kg car is beings coasting at 20 m/s along a level road . How large of a constant frictional force is required to stop it in a distance of 30m ?

Answer 1

Given data

*The given mass of the car is m = 900 kg

*The car is moving at a velocity is u = 20 m/s

*The given distance is s = 30 m

The formula for the acceleration of the car is given by the equation of motion as

`\begin{gathered} v^2=u^2+2as \\ a=(v^2-u^2)/(2s) \end{gathered}`

*Here v = 0 m/s is the final velocity of the car

Substitute the known values in the above expression as

`\begin{gathered} a=((0)^2-(20)^2)/(2*30) \\ =-6.67m/s^2 \end{gathered}`

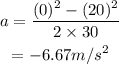
The formula for the frictional force is required to stop it at a distance of 30 m is given as

`f=ma`

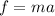
Substitute the known values in the above expression as

`\begin{gathered} f=(900)(-6.67) \\ =-6000\text{ N} \end{gathered}`

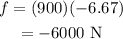
Hence, the frictional force is required to stop it at a distance of 30 m is f = -6000 N