Given:
Depth of the bottom = 11.0 km
Let's calculate the pressure due to the ocean at a depth of 10.6 km.
Apply the formula:
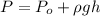
Where:
P is the pressure
ρ is the density of sea water = 1027 kg/m³
g is the acceleration due to gravity = 9.8 m/s²
h = 10.6 km = 19.6 x 10³ m
Po = 1 atm
Thus, we have:

Where:
1 atm = 101325 Pa
We have:
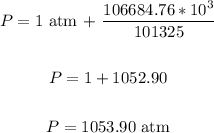
Therefore, the pressure due to the ocean at the depth of 10.6 km is 1053.90 atm.
ANSWER:
1053.90 atm