Question

The greatest ocean depths on the Earth are found in the Marianas Trench near the Philippines, where the depth of the bottom of the trench is about 11.0 km. Calculate the pressure due to the ocean at a depth of 10.6 km, assuming sea water density is constant all the way down. (The validity of the assumption of constant density is examined in one of the integrated concept problems.)

Answer 1

Given:

Depth of the bottom = 11.0 km

Let's calculate the pressure due to the ocean at a depth of 10.6 km.

Apply the formula:

`P=P_o+\rho gh`

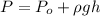
Where:

P is the pressure

ρ is the density of sea water = 1027 kg/m³

g is the acceleration due to gravity = 9.8 m/s²

h = 10.6 km = 19.6 x 10³ m

Po = 1 atm

Thus, we have:

`\begin{gathered} P=1\text{ atm+\lparen1027}*9.8*10.6*10^3) \\ \\ P=1\text{ atm+\lparen106684.76 *10}^3\text{\rparen} \end{gathered}`

Where:

1 atm = 101325 Pa

We have:

`\begin{gathered} P=1\text{ atm + }(106684.76*10^3)/(101325) \\ \\ P=1+1052.90 \\ \\ P=1053.90\text{ atm} \end{gathered}`

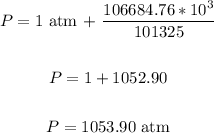
Therefore, the pressure due to the ocean at the depth of 10.6 km is 1053.90 atm.

ANSWER:

1053.90 atm