Question

The vertices of AJKL are J(1.3), K(4,4), and L(3,1). Graph AJKL and its image after a reflection in the line y = x.​

Answer 1

Answers:

• J ' (3, 1)
• K ' (4, 4)
• L ' (1, 3)
• The graph is shown below

=======================================================

Step-by-step explanation:

The rule to reflect over the line y = x is this

`(\text{x},\text{y})\to(\text{y},\text{x})`

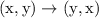
The x and y coordinates swap places. A point like (5,7) moves to (7,5) as an example.

When we apply that rule to the points J, K, L, we get the following

• J(1,3) moves to J ' (3,1)
• K(4,4) stays at (4,4) so K ' (4, 4)
• L(3,1) moves to L ' (1,3)

Then take note of these two facts:

1. Point K and point K' are at the same location. In other words, point K doesn't move. Points on the mirror line will not move when applying reflections.
2. Points J and L swap places since both involve coordinates 1 and 3 in either order.

Because of these two facts, triangle JKL and triangle J'K'L' occupy the same exact space and area. All that's happened really is almost all of the vertices have been relabeled to something else.

See below for the graph.