Question

Pls helpp!!!!!!!!!!!!!​

Answer 1

Answer: Yes

The point (-8,4) makes the inequality
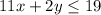`11x + 2y \le 19` true

==================================================

Step-by-step explanation:

We have x = -8 and y = 4 pair up together due to the point (x,y) = (-8,4).

Let's plug these values into the inequality

`11x + 2y \le 19\\\\11(-8) + 2(4) \le 19\\\\-88+8 \le 19\\\\-80 \le 19\\\\`

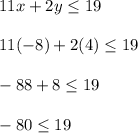
The last inequality is true because -80 is to the left of 19 on the number line. So -80 is smaller than 19.

Since the last inequality is true, this means the first inequality is true when (x,y) = (-8,4).