Question

Write an equation in standard form for the line describes below using only integers

Answer 1

y = -5x -17

Step-by-step explanation:

We were given the information:

`\begin{gathered} x-5y=2 \\ (-4,3) \end{gathered}`

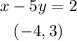
We will proceed to obtain the equation for the line:

`\begin{gathered} x-5y=2 \\ \text{Subtract ''x'' from both sides, we have:} \\ -5y=2-x \\ \text{Divide both sides by ''-5'', we have:} \\ y=-(2)/(5)-(1)/(-5)x \\ y=-(2)/(5)+(1)/(5)x \\ y=(1)/(5)x-(2)/(5) \\ \text{Comparing with the standard form, }y=mx+b,\text{ we have:} \\ mx=(1)/(5)x \\ slope(m)=(1)/(5) \end{gathered}`

We will proceed as follows:

`\begin{gathered} \text{For a perpendicula}r\text{ line, the slope is given by:} \\ m_(perpendicular)=-(1)/(m) \\ m_(perpendicular)=-(1)/((1)/(5)) \\ m_(perpendicular)=-5 \\ \text{The perpendicular line lies on the point (-4, 3). Using the point-slope equation, we have:} \\ y-y_1=m_{}(x-x_1)\Rightarrow y-y_1=m_(perpendicular)(x-x_1) \\ (x_1,y_1)=(-4,3) \\ y-3=-5(x--4) \\ y-3=-5(x+4) \\ y-3=-5x-20 \\ \text{Add ''3'' to both sides, we have:} \\ y=-5x-20+3 \\ y=-5x-17 \\ \\ \therefore y=-5x-17 \end{gathered}`

Therefore, the equation of the perpendicular line to that equation that lies on the point (-4, 3) is: y = -5x -17